[99클럽 코테 스터디 2일차 TIL] 피보나치 비스무리한 수열
2025. 4. 1. 16:22ㆍAlgorithm
✔️ 오늘의 키워드
- dp
- 메모이제이션
- dfs
✔️ 문제 및 풀이
피보나치 수열 문제와 거의 동일하고 n <= 116 이었기 때문에 어렵지 않은 문제였으나 자료형 long 을 사용하지 않고 int 를 사용하다가 헤맸던 문제다.
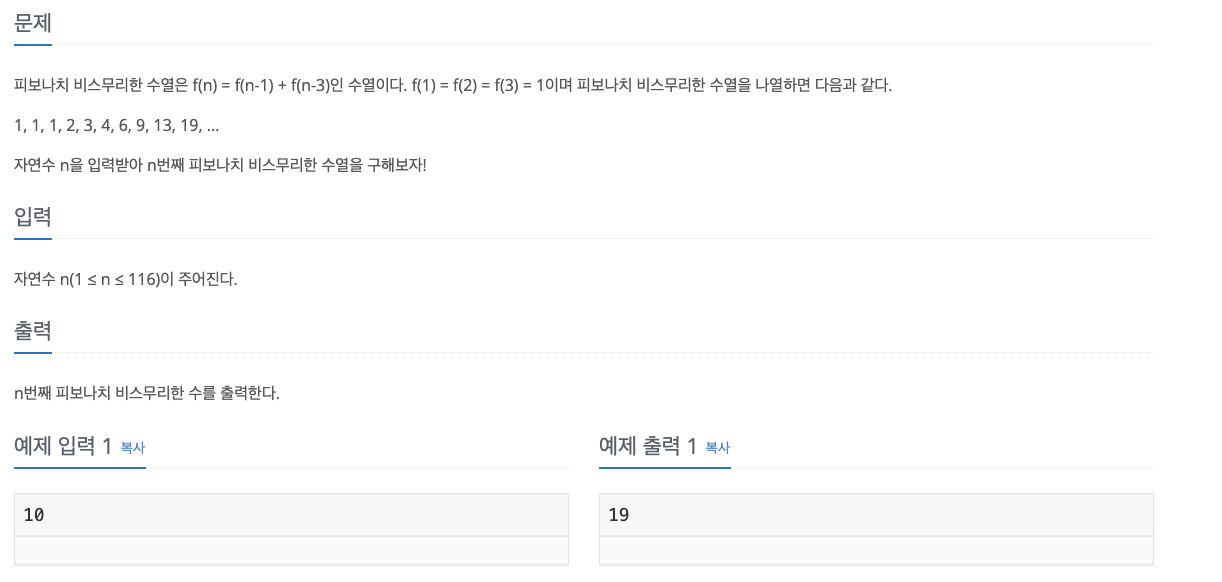
나는 일단 두가지 방식으로 풀어보았다.
1. dfs() with memoization
입력 : 자연수 n (1~116)
로직 : dfs를 사용하여 재귀적으로 탐색, 중복 계산 방지를 위해 배열에 결과 저장 , f(n) = f(n-1) + f(n-3)연산 수행
메모이 제이션을 활용하지 않고 재귀로만 구현했다면 O(2^n)이었겠지만 메모이제이션을 활용하여 중복된 연산을 수행하지 않음. 즉, Cache 값이 없는 경우에만 연산을 수행한다는 것이다. => O(n)
출력 : 피보나치 비스무리한 수열 f(n) = f(n-1) + f(n-3)의 결과
2. dp
입력 : 자연수 n (1~116)
로직 : 4~최대 116까지 반복문을 돌면서 dp 연산 수행 => O(n)
출력 : 피보나치 비스무리한 수열 f(n) = f(n-1) + f(n-3)의 결과
그러나 재귀시 함수 호출 스택등을 고려한다면 dp와 같이 반복문을 활용하는 것이 조금더 효율적일 것이라고 예상
1. 메모이제이션 없이 재귀적으로만 구현 했을 떄 - 시간초과 발생 O(2^n)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.sql.PreparedStatement;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 입력 : 자연수 n (1~116)
String readLine = br.readLine();
Integer input = Integer.parseInt(readLine);
int result = dfs(input);
// 출력 : 피보나치 비스무리한 수열 f(n) = f(n-1) + f(n-3)의 결과
System.out.println(result);
}
public static int dfs(int n) {
// dfs exit 조건
if (n == 1 || n == 2 || n == 3){
return 1;
}
return dfs(n-1) + dfs(n-3);
}
}
2. 메모이제이션 사용 - O(n)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.sql.PreparedStatement;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 입력 : 자연수 n (1~116)
String readLine = br.readLine();
Integer input = Integer.parseInt(readLine);
// 로직 : dfs를 사용하여 재귀적으로 탐색, 중복 계산 방지를 위해 배열에 결과 저장
long[] dp = new long[117];
int[] visited = new int[117];
long result = dfs(input, dp , visited);
// 출력 : 피보나치 비스무리한 수열 f(n) = f(n-1) + f(n-3)의 결과
System.out.println(result);
}
public static long dfs(int n, long[] dp, int[] visited ) {
// dfs exit 조건
if (n == 1 || n == 2 || n == 3){
dp[n] = 1;
visited[n] = 1;
return 1;
}
if (visited[n] == 1 ) {
return dp[n];
}
dp[n] = dfs(n-1, dp, visited) + dfs(n-3, dp, visited);
visited[n] = 1;
return dp[n];
}
}
3. dp - O(n)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.sql.PreparedStatement;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 입력 : 자연수 n (1~116)
String readLine = br.readLine();
int input = Integer.parseInt(readLine);
// 로직 : dp사용하여 배열에 결과 저장
long [] dp = new long[117];
dp[1] = dp[2] = dp[3] = 1;
for (int i = 4; i <= input; i++) {
dp[i] = dp[i - 1] + dp[i - 3];
}
// 출력 : 피보나치 비스무리한 수열 f(n) = f(n-1) + f(n-3)의 결과
System.out.println(dp[input]);
}
}
✔️ 회고
결과 값이 매우 커질 수 있을때는 long으로 받을 수 있도록 유의해야겠다.
int 형
- 32bit(=4byte)
- 정수를 나타내는 데이터 타입
- 범위 : -2147483648 ~ 2147483647
long 형
- 64bit(=8byte)
- 정수를 나타내는 데이터 타입
- 범위 : -9223372036854775808 ~ 9223372036854775807
- int형에 비해 많은 메모리를 필요로 하고 속도도 느림

'Algorithm' 카테고리의 다른 글
| [99클럽 코테스터디 5일차 TIL] 수열 (슬라이딩 윈도우) (0) | 2025.04.04 |
|---|---|
| [99클럽 코테 스터디 3일차 TIL] 바탕화면 정리 (0) | 2025.04.04 |
| [99클럽 코테 스터디 1일차 TIL] Top K Frequent Elements (0) | 2025.03.31 |
| [알고리즘 | 프로그래머스] 게임 맵 최단 거리(BFS) (0) | 2025.03.21 |
| [알고리즘 | 백준 ] 9934번 _ 완전 이진 트리 (0) | 2025.03.11 |